|
SCIENTIFIC APPROACHES TO
CATCH A LION

CONTENT

CATCHING LIONS ON A DALMATIAN PAGE?
 |
Of course lions as kind of "meta cats" belong to a real cats and dogs site. But to explain
the deeper reason I have to go back a bit *takeadeepbreath*: as you might know I'm extremely curious and have a weakness for stars and space stuff
too. Fine, but was have the stars to do with lions (apart from the fact that of course one see stars if the lion hits you with his paw on the head)?
Okay, beside the stars I also thought that it's very dubious that things tend to falling to the
ground. When I was a child they explained to me that objects attract each other (no, that wasn't the sex education). Later I heard that this can be
explained with Newtons law of gravity.
Of course that wasn't enough for me. Shure - with it you can well CALCULATE the graviation,
but only a fool would put up with that. I wanted to UNDERSTAND it. In time it became clear to me that it's not that easy:
a strange force like the gravitation where objects have a direct effect to other bodies doesn't exist at all. But still the apples don't keep to that and remain
falling from the trees. But how can they do that? And why? My investigations lead me to space and time (wow). The reason for the behaviour of the apple has a lot to
do with the space-time - and now it started fascinating me totally because with that it concerns one of my favorite topics: the stars.
The whole thing turned to be more and more interesting. I - as a non physicist - was suddenly
confronted with the theory of relativity and other strange things. You won't believe: it's more exiting than every crime thriller (altough I don't claim to
have it understood) and it's very inspiring to imagine all those things...
One day during my "research" in the internet I found in a search engine interesting hints
about this and (very strange) how the theory of relativity can be helpful for catching lions in the sahara.
The origin of this was
"A contribution to the mathematical theory of big game hunting" in the American Mathematical Monthly 1938 by "H. Petard, of Princeton NJ" [Ralph Boas]
and in Europe "Humor in der Mathematik" by Friedrich Wille (bei Vandenhoek & Ruprecht, Göttingen) which was over the years complemented with
various funny contributions of the net comunity.
Oh guys, what did I have to laugh! This is so clever and funny, therefore I cant's resist
to put it on my page too (although it's of course an absolute "oldie").
Also if you're not familiar with physics or mathematics - it's absolutely not neccesary to understand every detail (the one or the other thing will look
familiar for shure). So it's very amusing to imagine that a lion will be very stretched and flat if you move with near speed of light what allows you to
neat rool up the lion and fix it with an elastic band :-)
Okay, enough waffling - let's go now! I wish lot's of fun discovering this methods to catch a lion. |
 |
INTRODUCTION
 |
Since the realization of the well known, spectacular, quantum mechanic though experiment
cats (especially schrödinger cats) have an affinity to physics and mathematics.
In order to maintain the supplies of virtual though-laboratory animals it's essential to catch the
animals also in the theory.
As the pride of creation, ups sorry, the king of the cats (or something like this) the lion shall, in the following
survey of methods, be treated exemplary for similar cases.
|
 |
PREAMBEL AND WARNING
 |
Most methods assume that there's at least one lion in the desert. This of course is a permissible,
physical sensible hypothesis.
In order that it continues to be like that (and due to the international settlement for the protection of
endangered species and general thoughts of the protection of animals) this methods should be applied only to mental experiments.
Any similarities to real existing animals and persons living or dead are purely coincidental but inevitable. During the
development of the methods no non-virtual animals (neither lions nor others) was hurt or treated not suitable for animals.
|
 |
PHYSICS METHODS
 |
1. |
THE NEWTON GRAVITATION METHOD
Cage and lion attract each other with the gravitation force. We neglect the friction. This way the lion will arive sooner or later in the cage. |
| 2. |
THE NEWTON THIRD LAW METHOD
Let the lion catch you (let's assume you remain alive here). For every action there is an equal and opposite reaction. Therefore, you will have captured the lion. |
| 3. |
THE HEISENBERG METHOD
Position and Velocity from a moving lion can not be measure at the same time. As moving lions have no physical meaningfull position in the desert, one can not catch them. The lion hunt can therefore be limited to resting lions. The catching of a resting, not moving lion is left as an exercise for the reader. |
| 4. |
THE SCHROEDINGER METHOD
At every instant there is a non-zero probability of the lion being in the cage. Sit and wait. |
| 5. |
THE THERMODYNAMICS METHOD
We construct a semi-permeable membrane which lets everything but lions pass through. This we drag across the desert. |
| 6. |
THE SPECIAL RELATIVISTIC METHOD
One moves over the desert with light velocity. The relativistic length contraction makes the lion flat as paper. One takes it, rolls it up and puts a rubber band around the lion. |
| 7. |
THE MAGNETO-OPTICAL METHOD
We plant a large, lense shaped field with cat mint (nepeta cataria) such that its axis is parallel to the direction of the horizontal component of the earth's magnetic field. We put the cage in one of the field's foci . Throughout the desert we distribute large amounts of magnetized spinach (spinacia oleracea) which has, as everybody knows, a high iron content. The spinach is eaten by vegetarian desert inhabitants which in turn are eaten by the lions. Afterwards the lions are oriented parallel to the earth's magnetic field and the resulting lion beam is focussed on the cage by the cat mint lense. |
| 8. |
THE METHODE OF PARALLELS
Select a point in the desert and introduce a tame lion not passing through that point. There are three cases:
- The geometry is Euclidean. There is then a unique parallel lion passing through the selected point. Grab it as it passes.
- The geometry is hyperbolic. The same method will now catch infinitely many lions.
- The geometry is elliptic. There are no parallel lions, so every lion meets every other lion. Follow a tame lion and catch all the lions it meets: in this way every lion in the desert will be captured.
|
 |
MATHEMATICAL METHODS
 |
1. |
THE HILBERT (AXIOMATIC) METHOD
We place a locked cage onto a given point in the desert. After that we introduce the following logical system:
Axiom 1: The set of lions in the Sahara is not empty.
Axiom 2: If there exists a lion in the Sahara, then there exists a lion in the cage.
Procedure:If p is a theorem, and if the followin is holds: "p implies q", then q is a theorem.
Theorem: There exists a lion in the cage. |
| 2. |
THE GEOMETRICAL INVERSION METHOD
We place a spherical cage in the desert, enter it and lock it from inside.
Case 1: The lion is inside the cage. This case is trivial.
Case 2: The lion is outside the cage. We then perform an inversion with respect to the cage. Then the lion is inside the cage, and we are outside.
Warning: With this method, it is important not to stand in the middle of the cage, as one will disappear in the infinite. |
| 3. |
THE PROJECTIVE GEOMETRY METHOD
Without loss of generality, we can view the desert as a plane surface.
We project the surface onto a line and afterwards the line onto an interior point of the cage. Thereby the lion is mapped onto that same point. |
| 4. |
THE BOLZANO-WEIERSTRASS METHOD
Divide the desert by a line running from north to south. The lion is
then either in the eastern or in the western part. Let's assume it is in the eastern part. Divide this part by a line running from east to west. The lion is either in the northern or in the southern part. Let's assume it is in the northern part. We can continue this process arbitrarily and thereby constructing with each step an increasingly narrow fence around the selected area. The diameter of the chosen partitions converges to zero so that the lion is caged into a fence of arbitrarily small diameter.
Warning: With this method take care that the beautifull skin of the lion is not damaged. |
| 5. |
THE SET THEORETICAL METHOD
We observe that the desert is a separable space.
It therefore
contains an enumerable dense set of points which constitutes a sequence with the lion as its limit. With a cage on our backs,
we jump from point to point of this sequence an so approach the lion as near as we like. |
| 6. |
THE PEANO METHOD
In the usual way construct a curve containing every point in the
desert. It has been proven [1] that such a curve can be traversed in arbitrarily short time. Now we traverse the curve, carrying a spear,
in a time less than what it takes the lion to move a distance equal to its own length. |
| 7. |
A TOPOLOGICAL METHOD
We observe that the lion possesses the topological gender of a torus. We embed the desert in a four dimensional space. Then it is possible to apply a deformation [2] of such a kind that the lion when returning to the three dimensional space is all tied up in itself. It is then completely helpless. |
| 8. |
THE CAUCHY METHOD
We examine a lion-valued function f.
Be z the cage.
Consider the integral
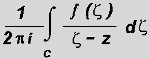
where C represents the boundary of the desert.
Its value is f(z), i.e. there is a lion in the cage. |
| 9. |
THE BANACHSCHE OR ITERATIVE METHOD
Let f be a contraction of the Sahara in it with contraction point x0.
On this point we put the cage. By successive iteration
Wn+1 = f(Wn), n = 0,1,2, ... ( W0 = Sahara )
the Sahara will be contracted to x0. In this way the lion will get in the cage. |
| 10. |
THE INDUCTIVE METHOD
Initial Condition: If you center a large cage on any one
grain of sand, and a lion is on or close to the grain of sand. Then he will be trapped by the cage. By close we mean within epsilon
grains of sand. Given a cage the size of 2 * (size of lion * epsilon) it works.
First Hypothesis: Given the first grain of sand in the desert, if the lion is standing on it you will trap him.
Proof: Given by the initial condition.
Induction Hypothesis: Assume that a lion is on a grain of sand n, and is trappable. Now, for grain n+1 (assume all grains of sand
are ordered, inorder) n+1 is close to n, hence n is close to n+1. If the lion is on grain n, and is trappable; then he is close to n+1, and by the
above condition, trappable. Hence, no matter where the lions are if you drop a cage centered on a piece of sand you will catch a lion.
|
 |
VARIOUS METHODS
 |
1. |
THE ARCHAELOGICAL METHOD
In order that an archaeologist can find the lion it has to be at least 90 feet under the ground. |
| 2. |
THE PENTAGON METHOD
Construct a safe, secure cage and leave the door open. Alternate massive B-52 strikes across the Sahara desert with subtle propaganda campaigns emphasizing the safety and security of your cage. When a lion enters the cage, close and lock the door. |
| 3. |
THE SUPPLY-SIDE METHOD
Distribute vast quantities of lion food and eliminate all threats to the lion population. Put a cage in the desert and wait for the explosive growth of the lion population to force a lion into the cage. |
| 4. |
THE MARXIST-LENINIST METHOD
Indoctrinate the gazelle population of the Sahara desert in dialectical materialism. Disguise your cage as a re-education camp for capitalist lions, and the gazelles will bring you all the lions you need.
|
 |
COMPUTER SCIENCE METHODS
 |
1. |
THE STANDARD APPROACH
We know what a Lion is from ISO 4711/X.123. Since CCITT have specified a Lion to be a particular option of a cat, we will have to wait for a harmonised standard to appear. Funding worth 10,000,000 pounds has been provided for initial investigations into this standard's development. |
| 2. |
THE UNIX METHOD
We release as much as possible animals into the Sahara (well suitable for it are gnus, yaks or mussels). The more animals are walking around the slower is each one.
With that the lion will be very slow and you can gentle build a cage around it. Hint: the younger the Sahara is, the more animals are needed!
In some very old Saharas it might happen, that you can't release an animal at all! |
| 3. |
THE WINDOWS METHOD
In this simplified variant of the Unix method one single window takes the part of the various animals. Important is here: the newer the windows the slower the lion.
Caution: it can happen very easily that this window uses all the space of the Sahara and neither cage nor lion won't fit in anymore.
Usually this problem can be avoid with some additional or extended Sahara. |
| 4. |
ANOTHER UNIX METHOD
Put the lion on (the hard) disk
Do :
ls -l | grep -i "lion" | cut $9 > trapfile< br>-i option ensures that size of the lion does not matter.
Now the lion is caught in a trapfile, and can be safely tar-ed or backed up ....into tape ! |
| 5. |
THE LOST OBJECTS METHOD
Make a linked list of all objects in the desert. Then delete the pointers on either side of the lion.(Make sure you are not AFTER the lion.) |
| 6. |
THE DEADLOCK TRAP
In the Sahara you fix a steak or something in a way that at one time only one lion could get it. Of course more lions will smell the steak and want to get it - but no one can. This way all lions will be caught in the deadlock trap.
Advantage: you catch all lions at the same time.
Disadvantage: unfortunately this method won't work if there's just one lion available in the Sahara. Should this be the case, a lion must be borrowed from the next zoo. With this we have reduced the problem to a known one. |
| 7. |
THE MS-DOS METHOD
You move the sahara including the lion to the directory C:\SAHARA and delete it afterwards from the map with DEL *.*. Then you remove everything in the directory C:\SAHARA except the lion with commands like DEL SAND.SND, DEL PLANTS.PLT and similar things. Now you copy the directory including the lion to a floppy in drive A: (COPY C:\SAHARA\*.* A:). It's very important to copy all lion files in order to keep the functions of all organs and the lion itself alive.
This disc can be printed out without problems at the next copyshop, it's also a decorative hunting trophy on the wall. Hint: the harddisk and the floppy to be used should be checked before with CHKDSK.EXE /F resp. SCANDISK.EXE (MS-DOS 6.xx and higher) for possible errors in order to avoid damages on the lion. For reasons of space the floppy should contain no other data.
Greenpeace and various conservation groups are strictly against the usage of this method because of the fast removal of all deserts on the maps. |
| 8. |
THE KI METHOD
search(lion,sahara,_) :- var(sahara),!,fail.
% in a not instatiated sahara
% you cant catch lions.
search(lion,sahara,sahara) :- atomic(sahara),
found(lion,sahara).
% If the desert is atomic,
% there has to be the lion.
search(lion,[],_):- !, fail.
% If the desert is empty, there is also
% no lion in it.
search(lion,[HEAD],HEAD) :- found(lion,HEAD).
% If the lion is in first element
% of desert, then stop.
suche(lion,[_|T],X) :- search(lion,T,X).
% Else continue search.
catch(What,Where,With_What) :-
catch(What,Where,WhereExactly),
move(With_What,WhereExactly).
found(What,In_What) :- member(What,In_What).
move(What, _ ) :- retract(position(What,_)), fail.
move(What,Where_To) :- asserta(position(What,Where_To)).
test_sahara([sahara_1, sahara_2, sahara_3, sahara_4, sahara_5,
sahara_6, sahara_7, [sahara_8, lion], sahara_9,
sahara_A, [sahara_B, risk], sahara_C, sahara_D]).
catch_lion_test :-
move(cage,risk),
test_sahara(sahara),
catch(lion,sahara,cage).
|
| 9. |
ITERATIVE METHODS
! Suitable data structures have to be provided !
- As a standard solution the following is recommended:
MODULE catch;
FROM problem IMPORT solution;
BEGIN;
solution;
END catch.
- Also possible in ASM (MS-DOS) (MASM 9.0 and higher or TASM 4.5 and higher):
dosseg
.DATA
MAX equ 65535
sahara_Field db MAX dup (0)
cage db
extern lion_Fkt_Number:Word ; DOS-Int. number
.CODE
lds si, W_Field ; ES:DI points to beginning
cld ; of field
mov CX,MAX ; CX as max. index
M1:
lodsb
cmp al,lion
je caught
loop M1
jmp Error
caught:
mov BX,SI
mov AX,lion_Fkt_Number
lds di, cage
int 21h ; DOS-Interrupt because all
; large Proc. have to be
Error: ; placed in ASM.
int 20h
END
|
| 10. |
THE TEXTADVENTURE METHOD
 The unique real solution which really works can be found in the genious environment of LPC
in UNItopia
/* it's a multi user textadventure written in C++-Clone. */
{ Advert : login telnet 129.69.221.120 3333 and play }
The unique real solution which really works can be found in the genious environment of LPC
in UNItopia
/* it's a multi user textadventure written in C++-Clone. */
{ Advert : login telnet 129.69.221.120 3333 and play }
int fang(string str)
{ object ob1,ob2,ob3;
if (!str || str!="lion mit cage")
{ write("WHOM do you want to catch with WHAT ?\n");
return 1;
}
ob1=clone_object("/obj/sahara"); /* sahara includes lion */
ob2=clone_object("/obj/cage"); /* see problem */
if (!ob3=present("lion",ob1)
{ write("It's no lion in the sahara!\n"); /* if escaped */
return 1;
}
ob3->move(ob2);
write("The lion is now in the cage.\n");
return 1;
}
This function has to be connected to an event, the objects
cage.c and sahara.c are suitable to be implemented.
In Turbo Pascal it works of course too:
program Test_Solution;
type sahara_Typ = Array[1..Max_X,1..Max_Y] of Index;
Inhalt = { don't know }
cage_Typ = record
voll : Boolean;
Inhalt : Animal;
end;
lionn_Typ = Animal;
var sahara : sahara_Typ;
cage : cage_Typ;
Animal : Array[1..Max_Animal] of Animal; { If also }
{ camels in the }
procedure lion_Catch; { sahara available. }
var i,j:Word;
begin;
cage.voll:=false;
for i:=1 to Max_X do { search lion in sahara }
for j:=1 to Max_Y do
if sahara[i,j]=lionN_INDEX then begin;
cage.Inhalt:=Animal[sahara[i,j]];
cage.voll:=true;
sahara[i,j]:=NO_INDEX;
exit; { Because cage is full }
end; { One could catch all }
{ lions with this procedure. }
WriteLn('Attention! No lion found, how about a camel?');
end;
begin;
Init; { sahara, Animal terminated. }
lionn_Fang;
if (cage.voll) then WriteLn('Ok, the lion is in the cage.')
else WriteLn('Attention! No lion found, with "+
'changes in CAMEL_INDEX maybe"+
#10#13'a camel could be possible too ?');
end.
Even as Shellscript it works now:
#!/bin/sh
for $animal in $sahara
do
if [ $animal = $lion ]
then mv $animal $cage; exit 0
fi
done

|
 |
|

|