|
WISSENSCHAFTLICHE ANSÄTZE FÜR
DIE ERFOLGREICHE
LÖWENJAGD

INHALTSVERZEICHNIS

WAS HAT DIE LÖWENJAGD HIER ZU SUCHEN?
 |
Natürlich gehören Löwen als Überkatzen schon auch auf eine richtige Katzen- und
Hundeseite. Aber um den eigentlichen Grund zu erklären, muss ich etwas ausholen *tieflufthol*: wie ihr wisst bin ich ein extrem neugieriger Mensch und habe auch
ein Faible für die Sterne... Gut, was haben aber Sterne mit Löwen zu tun (abgesehen von der Tatsache dass man bestimmt Sterne sieht, wenn der
Löwe einem mit seiner Pranke ordentlich auf den Kopf kloppt)?
Also mir war es - mal ganz abgesehen von Sternen - schon immer etwas suspekt erschienen, warum Dinge stark dazu neigen, zu Boden zu
fallen. Als Kind hat man mir erklärt, dass sich Körper halt einfach anziehen (nein, das war nicht bei der Aufklärung!). Später hiess es dann, dies könne
durch das Newtonsche Gravitationsgesetz erklärt werden.
Das war mir natürlich nicht genug. Natürlich kann man nun die Gravitation wunderbar ERRECHNEN - aber nur ein Narr gibt sich damit zufrieden. Ich wollte
es VERSTEHEN. Mit der Zeit wurde klar, dass es nicht ganz so einfach ist (Newton in Ehren): hat doch die Gravitation unheimlich viel mit Raumkrümmung und ZEIT (!) zu
tun. Mit der Raumzeit also, womit wir einerseits bei Einstein und Wheeler angelangt wären und zum anderen war ich nun völlig im Element weil es nun
auch eines meiner Lieblingsthemengebiete, die Sterne, betraf.
Das Ganze wurde viel spannender für mich als jeder Kriminalroman - es ist echt abenteuerlich diese Dinge kennenzulernen und ein richtiges
"Gehirntraining" diese auch verstehen zu wollen - welchen Anspruch ich natürlich nicht erhebe ;-)
Irgendwann auf meinen Nachforschungs-Streizügen durchs Internet fand ich plötzlich in einer Suchmaschine Hinweise darauf, wie einem die Quantenphysik
(wo natürlich die ganzen Gesetze welche ich meinte langsam zu begreifen wieder komplett über den Haufen geworfen werden) und auch die
Relativitätstheorie nützlich beim Löwenfangen sein können.
Der eigentliche Ursprung geht vermutlich auf "A contribution to the mathematical theory of big
game hunting" in the American Mathematical Monthly 1938 von "H. Petard, of Princeton NJ" [Ralph Boas] und neueren Datums auf
"Humor in der Mathematik" von Friedrich Wille (erschienen bei Vandenhoek & Ruprecht, Göttingen) zurück, wurde aber im Laufe der Jahre durch die Internetgemeinschaft auf kreativste
Weise mannigfaltig ergänzt.
Leute, was habe ich gelacht! Dies ist sowas von geistreich und amüsant zugleich - da kann ich natürlich nicht wiederstehen (obwohl es in einigen Kreisen
sicher der absolute "Oldie" ist) dies auch auf meine Page zu legen.
Auch wenn Du Dich nicht mit Physik oder Mathematik beschäftigt hast - es ist durchaus nicht nötig alles nachzuvollziehen (das eine oder andere wird
Dir bestimmt noch bekannt vorkommen). So ist's doch wirklich witzig sich vorzustellen, dass ein Löwe sich bei Lichtgeschwindigkeit ja ungemein in die
Länge ziehen muss (Längenkontraktion) und dabei flach wie Papier wird, was uns erlaubt, ihn schön säuberlich zusammenzurollen und mit einem
Gummiband zu befestigen *lach*.
So, genug geschwafelt - es geht nun los und ich wünsche Euch auch viel Heiterkeit beim Studium dieser Methoden! |
 |
EINFÜHRUNG
 |
Spätestens seit Durchführung des bekannten, spektakulären, quantenmechanischen Gedankenexperiments haben Katzen, insbesonders Schrödingersche, eine besondere Affinität zu Physik und Mathematik.
Um den Nachschub an virtuellen Gedankenversuchstieren nicht abreissen zu lassen, ist es notwendig, die Tiere auch in der Theorie einzufangen.
Da der Löwe bekanntlich die Krone der Schöpfung, äh Pardon, der König der Katzen (oder so ähnlich) ist, soll er in der folgenden Methodenübersicht exemplarisch für ähnlich gelagerte Probleme behandelt werden.
|
 |
VORBEMERKUNGEN UND WARNUNGEN
 |
Die meisten Methoden gehen davon aus, dass es in Afrika bzw. der Wüste mindestens einen Löwen gibt. Dies ist sicherlich eine zulässige, physikalisch sinnvolle Annahme.
Damit das auch so bleibt (und wegen des Washingtoner Artenschutzabkommens sowie allgemeinen tierschutzrechtlichen Überlegungen) sollten die Methoden nur gedankenexperimentell angewandt werden.
Ähnlichkeiten zu real existierenden Tieren oder Methoden sind rein zufällig, waren aber unvermeidlich. Bei der Entwicklung der Methoden wurden keine nicht-virtuellen Tiere (weder Löwen noch sonstige) verletzt oder nicht artgerecht behandelt.
|
 |
PHYSIKALISCHE METHODEN
 |
1. |
DIE NEWTONSCHE METHODE
Käfig und Löwe ziehen sich durch die Gravitationskraft an. Wir vernachlässigen die Reibung. Auf diese Weise muß der Löwe früher oder später im Käfig landen. |
| 2. |
DIE HEISSENBERG-METHODE
Ort und Geschwindigkeit eines bewegten Löwen lassen sich nicht gleichzeitig bestimmen. Da bewegte Löwen also keinen physikalisch sinnvollen Ort einnehmen, kommen sie für die Jagd auch nicht in Frage. Die Löwenjagd kann sich daher nur auf ruhende Löwen beschränken. Das Einfangen eines ruhenden, bewegungslosen Löwen wird dem Leser als Übungsaufgabe überlassen. |
| 3. |
DIE SCHRÖDINGER METHODE
Die Wahrscheinlichkeit dafür, daß sich ein Löwe zu einem beliebigen Zeitpunkt im Käfig befindet ist größer als Null. Man setze sich vor den Käfig und warte.
Bemerkung: Hierbei wird üblicherweise vorausgesetzt, daß der Käfig offen ist und man ihn zuschlagen muß, wenn der Löwe drin ist. H. Schubert wies aber darauf hin, daß man den Käfig wegen des Tunneleffekts auch zulassen kann. Auf diese Weise kann man bei der elenden Warterei auch mal weggehen und ein Bierchen trinken. Aber nicht zu lange! Denn kluge Löwen, die den Tunneleffekt begriffen haben, verschwinden auch wieder. |
| 4. |
DIE EXPERIMENTALPHYSIKALISCHE METHODE
Man nehme eine semipermeable Membrane, die alles ausser dem Löwen durchlässt, und siebe damit die Wüste durch. |
| 5. |
DIE EINSTEINSCHE ODER RELATIVISTISCHE METHODE
Man überfliege die Wüste nahezu mit Lichtgeschwindigkeit. Durch die relativistische Längenkontraktion wird der Löwe flach wie Papier. Man greife ihn, rolle ihn auf, und mache ein Gummiband herum. |
| 6. |
DIE HAWKINS METHODE
Man lasse ein kleines schwarzes Loch in der Wüste anbringen und definiere dieses als Käfig. Nach kurzer Zeit wird sich der Löwe darin befinden. Allerdings muss damit gerechnet werden, dass der Löwe darin keine Haare mehr haben wird. |
| 7. |
DIE OPTISCHE METHODE
Man schaue durch ein umgedrehtes Fernglas auf den Löwen, nehme ihn mit einer Pinzette und lege ihn in eine Streichholzschachtel.
|
 |
MATHEMATISCHE METHODEN
 |
1. |
DIE HILBERTSCHE ODER AXIOMATISCHE METHODE
Man stellt einen Käfig in die Wüste und führt folgendes Axiomensystem ein:
Axiom 1: Die Menge der Löwen in der Wüste ist nicht leer.
Axiom 2: Sind Löwen in der Wüste, so ist auch ein Löwe im Käfig.
Schlußregel:Ist p ein richtiger Satz, und gilt "Wenn p, so q.",so ist auch q ein richtiger Satz.
Satz: Es ist ein Löwe im Käfig. |
| 2. |
DIE GEOMETRISCHE METHODE
Man stelle einen zylindrischen Käfig in die Wüste.
1. Fall: Der Löwe ist im Käfig. Dieser Fall ist trivial!
2. Fall: Der Löwe ist außerhalb des Käfigs. Dann stelle man sich in den Käfig und mache eine Inversion an den Käfigwänden. Auf diese Art und Weise gelangt der Löwe in den Käfig und man selbst nach draußen.
Achtung: Bei Anwendung dieser Methode ist darauf zu achten, daß man sich nicht in die Mitte des Käfigbodens stellt, da man sonst im Unendlichen verschwindet! |
| 3. |
DIE PROJEKTIONSMETHODE
Ohne Beschränkung der Allgemeinheit nehmen wir an, daß die Wüste eine Ebene ist. Wir projezieren sie auf eine Gerade durch den Käfig, und die Gerade auf einen Punkt im Käfig. Damit gelangt der Löwe in den Käfig. |
| 4. |
DIE BOLZANO-WEIERSTRASS-METHODE
Wir halbieren die Wüste in Nord-Süd-Richtung durch einen Zaun. Dann ist der Löwe entweder in der westlichen Hälfte oder östlichen Hälfte. Wir wollen annehmen, daß er in der westlichen Hälfte ist. Daraufhin halbieren wir diesen westlichen Teil durch einen Zaun in Ost-West-Richtung. Der Löwe ist entweder im nördlichen oder im südlichen Teil. Wir nehmen an, er ist im nördlichen. Auf diese Weise fahren wir fort. Der Durchmesser der Teile, die bei der Halbiererei entstehen, strebt gegen Null. Auf diese Weise wird der Löwe schließlich von einem Zaun beliebig kleiner Länge eingegrenzt.
Achtung: Bei dieser Methode achte man darauf, dass das schöne Fell des Löwen nicht beschädigt wird. |
| 5. |
DIE MENGENTHEORETISCHE METHODE
Die Punkte in der Wüste lassen sich wohlordnen. Ausgehend vom kleinsten Element erwischt man den Löwen durch transfinite Induktion.
Bemerkung: Diese Methode ist in Fachkreisen umstritten wegen der Verwendung des Wohlordnungssatzes bzw. des Auwahlaxioms. Wie so oft, hat auch die vorliegende Fragestellung zu einer fruchtbaren Entwicklung geführt. Dabei wurde schließlich eine sehr viel einfachere Methode entdeckt, die den genannten Mangel nicht aufweist: Man betrachte alle Teilmengen der Wüste, die den Löwen enthalten und bilde ihren Durchschnitt. Er enhält als einziges den Löwen.
(Bei dieser Durchschneiderei sollte lediglich darauf geachtet werden, daß das schöne Fell des Löwen nicht zerschnitten wird.) |
| 6. |
DIE FUNKTIONALANALYTISCHE METHODE
Die Wüste ist ein separabler Raum.
Er enthält daher eine abzählbare dichte Menge, aus der eine Folge ausgewählt werden kann, die gegen den Löwen konvergiert.
Mit einem Käfig auf dem Rücken springen wir von Punkt zu Punkt dieser Folge und nähern uns so dem Löwen beliebig genau. |
| 7. |
DIE PEANO METHODE
Man konstruiere eine Peano-Kurve durch die Wüste, also eine stetige Kurve, die durch jeden Punkt der Wüste geht.
Es ist gezeigt worden, daß man eine solche Kurve in beliebig kurzer Zeit durchlaufen kann.
Mit dem Käfig unterm Arm durchlaufe man die Kurve in kürzerer Zeit, als der Löwe benötigt, um sich um seine eigene Länge fortzubewegen. |
| 8. |
DIE TOPOLOGISCHE METHODE
Der Löwe kann topologisch als Torus aufgefaßt werden. Man transportiere die Wüste in den vierdimensionalen Raum. Es ist nun möglich die Wüste so zu deformieren, daß beim Rücktransport in den dreidimensionalen Raum der Löwe verknotet ist. Dann ist er hilflos. |
| 9. |
DIE CAUCHYSCHE ODER FUNKTIONENTHEORETISCHE METHODE
Wir betrachten eine regulärelöwenwertige Funktion f auf der Wüste.
Der Käfig stehe im Punkt z der Wüste.
Man bildet das Integral
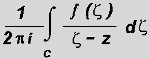
wobei C der Rand der Wüste ist.
Der Wert des Integrals ist f(z), d.h. es ist ein Löwe im Käfig. |
| 10. |
DIE BANACHSCHE ODER ITERATIVE METHODE
Es sei f eine Kontraktion der Wüste in sich. x0 sei ihr Fixpunkt.
Auf diesen Fixpunkt stellen wir den Käfig.
Durch sukzessive Iteration
Wn+1 = f(Wn), n = 0,1,2, ... ( W0 = Wüste )
wird die Wüste auf den Fixpunkt zusammengezogen.
So gelangt der Löwe in den Käfig. |
| 11. |
DIE KOMPAKTHEITSMETHODE
Die Wüste wird ohne Beschränkung der Allgemeinheit als kompakt vorausgesetzt.
Man überdecke sie mit einer Familie von Käfigen Ki (i aus I). Dann gibt es unter ihnen endlich viele Käfige, Ki1, ... ,in, die bereits die ganze Wüste überdecken.
Die Durchmusterung dieser Käfige wird als Diplomarbeit vergeben. |
| 12. |
DIE LOGISCHE METHODE ODER DIE METHODE DES TERTIUM NON DATUR
Man stelle einen offenen Käfig in die Wüste und lege ein Brett mit Leim daneben.
Beides biete man dem Löwen zum Betreten an. Der Löwe sagt dann: "Nein, auf den Leim gehe ich nicht!" Nach dem tertium non datur muß er in den Käfig gehen. Danach schlägt man die Tür zu. |
| 13. |
DIE STOCHASTISCHE METHODE
Man benötigt dazu ein Laplace-Rad, einige Würfel und eine Gaussche Glocke. Mit dem Laplace-Rad fährt man in die Wüste und wirft mit den Würfeln nach dem Löwen. Kommt er dann wutschnaubend angerannt, so stülpt man die Gaussche Glocke über ihn. Unter ihr ist er mit der Wahrscheinlichkeit eins gefangen. |
| 14. |
DIE DIDAKTISCHE METHODE
Man nähere sich dem Löwen auf der Brunnerschen Spirale. Dann elementarisiere man den Löwen zu einer Katze und fange ihn mit einer Schale Milch. |
| 15. |
DIE METHODE DER SCHWINGUNGSLEHRE
Man ermittle durch Versuche die Eigenresonanz des Löwen und rege ihn damit an. Schon nach kurzer Zeit wird sich die Resonanzkatastrophe bemerkbar machen. Kurz vor der Resonanzkatastrophe schalte man das schwingungserzeugende Gerät ab. Durch das Geschwinge und Geschucksel wir der Löwe so benommen sein, dass man ihm einreden kann, er sei eine Katze und ihn mit einem Spezialhalsband und einer Schuessel Milch nach Hause mitnehmen kann.
Anmerkung: Für die Anwendung dieser Methode ist die Anwesenheit eines Sicherheitsingenieurs erforderlich, der darauf achtet, dass der Löwe nicht durch zu heftige Resonanz zu Schaden kommt.
Erweiterte Resonanzmethode: Falls man richtig viel Energie zur Verfügung haben sollte, kann man auch einfach die Wueste selbst durch Schwingungen bis zur Resonanzkatastrophe anregen. Da sich dadurch die Wueste zerbröselt, fällt der Löwe einfach in den unter der freigemachten Wüste bereitgestellten Käfig hinein. |
| 16. |
DIE METHODE DER FESTIGKEITSLEHRE
Falls die Durchbiegung nicht vernachlässigbar ist, berechne man zunächst diese am Orte des Löwen. Dazu ermittle man zunaechst das Flächenintegral zweiten Grades der Wüste, das Biegemoment am Orte des Löwen sowie das Elastizitaetsmodul. Daraus erhalten wir mit Hilfe der Differentialgleichung der Biegelinie die Durchbiegung am Orte des Löwen. So dann berechne man die Kraft, die zusätzlich am Orte des Löwen nötig ist, damit sich die Wüste so weit durchbiegt, dass der Löwe vollständig in der entstandenen Senke verschwindet. Jetzt fülle man die entstandene Senke mit Wasser und bevor der Löwe jämmerlich ersauft, werfe man ihm einen Rettungsring zu. Der Löwe wird sich daran festhalten und man kann ihn aus dem Wasser in den bereitgestellten Käfig ziehen.
Voraussetzungen: Der Löwe ist Nichtschwimmer. Man hat vorher die Probleme "Wie finde ich Wasser in der Wüste", "Wie lasse ich einen Techniker einen Käfig bauen" und "Woher bekomme ich in der Wüste einen Rettungsring" erfolgreich gelöst. |
| 17. |
DIE GÖDELSCHE METHODE
Man konstruiere den Satz G für den Löwen. Diesen plaziert man in räumlicher Nähe zu einen geeigneten Stück Fleisch. Der Löwe wird das Fleisch finden und, da Löwen als intelligente Wesen beim Essen zu lesen pflegen, den Satz G lesen. Dies wird ihn zur Verzweiflung bringen und ihn völlig verwirren.
Den dergestalt hilflosen Löwen zu fangen ist trivial. Achtung: Diese Methode ist nicht ganz gefahrlos, da nicht sicher ist, welche Auswirkungen der Satz G für Löwen auf den Menschen hat. Andererseits ist es schwer, diesen Satz zu schreiben, ohne ihn zu denken! |
| 18. |
DIE METRISCHE METHODE
Wir stellen einen Käfig in die Wüste, verlassen diese unauffällig und definieren in ihr die indiskrete Metrik, d.h. der Abstand zwischen allen Punkten ist 0. Insbesondere ist also der Abstand zwischen Löwe und Käfig gleich 0, d.h. der Löwe ist im Käfig. |
| 19. |
DIE INDUKTIVE METHODE
Ein Löwe sei in der Wüste. Mit vollständiger Induktion zeigt man leicht, daß für beliebige natürliche Zahlen n gilt: n Löwen sind in der Wüste. Da die Wüste endlichdimensional und beschränkt ist und ein Löwe ein nach unten beschränktes Volumen hat, liegen die Löwen für hinreichend große n überall dicht, so daß zwangsläufig einer in den Käfig gedrängt wird.
|
 |
VERSCHIEDENE METHODEN
 |
1. |
DIE PHILOSOPHISCHE ODER DIE DIALEKTISCHE METHODE
Man zäunt die Wüste ein, bewässert sie, sät Gras und setzt Kaninchen aus. Die Kaninchen vermehren sich schnell. Nach Hegel kommt daher bald der Zeitpunkt, bei dem Quantität in Qualität umschlägt, und dann hat man einen Löwen. |
| 2. |
DIE ARCHÄOLOGISCHE METHODE
Damit Archäologen den Löwen finden, muss dieser sich mindestens 30 Meter unter der Erde befinden. |
| 3. |
DIE LEICHARDT'SCHE METHODE
Man fange sich in der Wüste ein Kamel. Anschliessend rede man solange wortgewandt auf das Kamel ein, bis es endlich zugibt, ein Löwe zu sein. |
| 4. |
DIE TELEKINETISCHE METHODE
Man laufe so lange durch die Wüste, bis man einen Löwen gefunden hat. Dann lache man sich einen Ast (in ausreichender Höhe), auf den man sich setze, um während der folgenden Aktion in Sicherheit zu sein, und staune Bauklötze, mit denen man sodann den Löwen bewirft, bis er ohnmächtig umfällt. |
| 5. |
EINGRIFF IN DIE FREIE MARKTWIRTSCHAFT
Man erhöhe nach Belieben Zinsen, Mieten und/oder Steuern in der Wüste. Gleichzeitig kann man Vergünstigungen für Löwen in Käfigen gewähren. Dem Löwen wird das Leben in der Wüste zu teuer und er wird sich freiwillig in den Käfig begeben. |
| 6. |
DIE SOZIALPÄDAGOGEN METHODE
Sozialpädagogen versuchen den Löwen zu verstehen. |
| 7. |
DIE U.S. ARMY METHODE
U.S. Army-Wissenschaftler entwickeln eine "L"-Bombe welche alle Fauna und Flora Afrikas bis auf die Löwen auslöscht, und schicken dann die Marines hinein, um den Rest (Löwe, Einwohner etc.) zu fangen. |
| 8. |
DIE TELEKOM METHODE
Hier macht man sich die Sozialkompetenz des Löwen zunutze. Man benötigt dazu nur eine Telefonzelle und eine Fahrradklingel. Die Telefonzelle wird in der Wüste aufgestellt und man klingelt mit der Fahrradklingel. Der Löwe hört das Klingeln, will ans Telefon und wenn er die Zelle betreten hat, muss man nur noch die Tür verschliessen. |
| 9. |
DIE HERLITZ METHODE
Man benötigt hierfür nur ein Notizblock der entsprechenden Firma. Damit setzt man sich auf eine Palme und wartet bis der Löwe sich unter diese legt. Nun zerreißt man den Notizblock und und läßt die Papierschnitzel auf den Löwen regnen. Der denkt es schneit und erfriert.
|
 |
METHODEN DER INFORMATIK
 |
1. |
DIE UNIX METHODE
Wir setzen möglichst viele Tiere in die Wüste (hervorragend hierfür eignen sich Gnus, Yaks oder Muscheln). Je mehr Tiere in der Wüste laufen, desto langsamer wird das einzelne. Damit wird der Löwe sehr langsam, und man kann ihm behutsam einen Käfig um ihn bauen. Hinweis: Je jünger die Wüste ist, desto mehr Tiere werden benötigt! In einigen sehr alten Wüsten kann es sogar passieren, dass man überhaupt kein weiteres Tier aussetzen kann! |
| 2. |
DIE WINDOWS METHODE
In dieser einfachen Variante der Unix-Methode erfüllt ein einziges Fenster die Rolle der vielen Tiere. Hierbei gilt: Je neuer das Fenster, desto langsamer der Löwe. Doch Vorsicht! Es kann leicht passieren, dass das Fenster sämtlichen Platz der Wüste beansprucht und weder Käfig noch Löwe hernach noch hineinpassen. Dieses Problem wird meistens dadurch umgangen, dass man durch die Beschaffung von etwas Zusatzwüste diese vergrössert. |
| 3. |
DIE DEADLOCK METHODE
Wir befestigen ein grosses Stück Fleisch an einem Ort in der Wüste, so dass nur jeweils ein Löwe gleichzeitig daran gelangen kann. Kommen nun mehrere Löwen gleichzeitig zum Fleisch, dann versuchen alle, es zu erreichen, doch keiner kann es. Alle Löwen sind damit in der Deadlock-Falle gefangen. Vorteil: Man fängt damit alle Löwen gleichzeitig! Nachteil: Die Methode funktioniert leider nicht, wenn nur ein einziger Löwe in der Wüste ist! Sollte dieser Fall eintreten, dann leihe man einen Löwen beim nächsten Zoo. Damit haben wir das Problem auf ein bekanntes zurückgeführt. |
| 4. |
DIE MS-DOS METHODE
Man verschiebt die Wüste samt Löwe in das Verzeichnis C:\WUESTE und löscht sie von der Landkarte mit DEL *.*. So dann löscht man im Verzeichnis C:\WUESTE alles ausser den Löwen mit Befehlen wie DEL SAND.SND, DEL PFLANZEN.PLT, und ähnlichem. Jetzt kopiert man das Verzeichnis samt Löwe auf eine Diskette im Laufwerk A: (COPY C:\WUESTE\*.* A:). Man sollte darauf achten. dass man alle Löwendateien kopiert, damit der Löwe alle Organe und Funktionen beibehält. Diese Diskette kann man problemlos beim nächsten Copyshop ausdrucken lassen oder sich die als Jagdtrophäe an die Wand hängen. Hinweis: Die Festplatte und die benutzte Diskette sollten vorher mit CHKDSK.EXE /F bzw. SCANDISK.EXE (ab MS-DOS 6.xx) auf mögliche Datenträgerfehler überprüft werden, um Beschädigungen am Löwen zu vermeiden. Die Diskette sollte aus Platzgründen keine anderen Daten enthalten. Greenpeace und verschiedene Umweltschutzorganisationen haben sich gegen die Verwendung dieser Fangmethode ausgesprochen, da dadurch bald alle Wüsten von der Landkarte verschwunden sein werden. |
| 5. |
DIE VIRUS METHODE
Virenprogrammierer setzen eine Maus am südlichen Ende der Wüste aus und warten im Norden auf den in Panik geratenen Löwen. |
| 6. |
DIE KI METHODE
suche(Löwe,Wüste,_) :- var(Wüste),!,fail.
% In einer nicht instantiierten W"uste
% lassen sich keine L"owen fangen.
suche(Löwe,Wüste,Wüste) :- atomic(Wüste), gefunden(Löwe,Wüste).
% Wenn die W"uste atomar ist,
% mu"s dort der L"owe sein.
suche(Löwe,[],_):- !, fail.
% Wenn die W"uste leer ist, ist auch
% kein L"owe drin.
suche(Löwe,[HEAD],HEAD) :- gefunden(Löwe,HEAD).
% Wenn der L"owe im ersten Element
% der W"uste ist, dann fertig.
suche(Löwe,[_|T],X) :- suche(Löwe,T,X).
% Sonst weiter schauen.
fange(Was,Wo,Womit) :-
fange(Was,Wo,WoGenau),
bewege(Womit,WoGenau).
gefunden(Was,Worin) :- member(Was, Worin).
bewege(Was, _ ) :- retract(position(Was,_)), fail.
bewege(Was,Wohin) :- asserta(position(Was,Wohin)).
test_Wüste([Wüste_1, Wüste_2, Wüste_3, Wüste_4, Wüste_5,
Wüste_6, Wüste_7, [Wüste_8, Löwe], Wüste_9,
Wüste_A, [Wüste_B, wagen], Wüste_C, Wüste_D]).
fange_Löwe_test :-
bewege(Käfig,wagen),
test_Wüste(Wüste),
fange(Löwe,Wüste,Käfig).
|
| 7. |
ITERATIVE METHODEN
! Geeignete Datenstrukturen werden vorausgesetzt !
- Als Standardlösung ist immer zu empfehlen:
MODULE Fang;
FROM Problem IMPORT Loesung;
BEGIN;
Loesung;
END Fang.
- Auch in ASM (MS-DOS) ist es möglich (ab MASM 9.0 oder TASM 4.5):
dosseg
.DATA
MAX equ 65535
Wüsten_Feld db MAX dup (0)
Käfig db
extern Löwe_Fkt_Nummer:Word ; DOS-Int. Nummer
.CODE
lds si, W_Feld ; ES:DI zeigt auf Anfang des Feldes
cld
mov CX,MAX ; CX als max. Index
M1:
lodsb
cmp al,Löwe
je Gefangen
loop M1
jmp Error
Gefangen:
mov BX,SI
mov AX,Löwe_Fkt_Nummer
lds di, Käfig
int 21h ; DOS-Interrupt, da alle aufwendigen
; Proc. in ASM ausgelagert
; werden sollen.
Error:
int 20h
END
|
| 8. |
DIE TEXTADVENTURE METHODE
 Die einzige wahrhaftige Lösung , die wirklich funktioniert , ist in
der genialen Umgebung des LPC, das man in UNItopia bewundern kann.
/* Ist ein Multi-User-Textadventures, geschrieben in C++-Clone. */
{ Werbung : einloggen unter telnet 129.69.221.120 3333 und spielen }
Die einzige wahrhaftige Lösung , die wirklich funktioniert , ist in
der genialen Umgebung des LPC, das man in UNItopia bewundern kann.
/* Ist ein Multi-User-Textadventures, geschrieben in C++-Clone. */
{ Werbung : einloggen unter telnet 129.69.221.120 3333 und spielen }
int fang(string str)
{ object ob1,ob2,ob3;
if (!str || str!="Löwe mit Käfig")
{ write("WEN willst du mit WAS fangen ?\n");
return 1;
}
ob1=clone_object("/obj/Wüste"); /* Wüste enthält Löwe s.Aufgabe */
ob2=clone_object("/obj/Käfig");
if (!ob3=present("Löwe",ob1)
{ write("Es ist kein Löwe in der Wüste!\n"); /* Falls weggerannt */
return 1;
}
ob3->move(ob2);
write("Der Löwe befinde sich jetzt im Käfig.\n");
return 1;
}
Diese Funktion muß noch an ein Ereignis angehängt werden, die Objekte
Käfig.c und Wüste.c sind geeignet zu implementieren.
In Turbo Pascal geht dieses Problem natürlich auch:
program Test_Loesung;
type Wüster_Typ = Array[1..Max_X,1..Max_Y] of Index;
Inhalt = { weiß nicht }
Käfig_Typ = record
voll : Boolean;
Inhalt : Tier;
end;
Löwen_Typ = Tier;
var Wüste : Wüster_Typ;
Käfig : Käfig_Typ;
Tiere : Array[1..Max_Tiere] of Tier; { Falls noch Kamele }
{ in der Wüste sind. }
procedure Löwen_Fang;
var i,j:Word;
begin;
Käfig.voll:=false;
for i:=1 to Max_X do { Wüste nach Löwe absuchen }
for j:=1 to Max_Y do
if Wüste[i,j]=LöweN_INDEX then begin;
Käfig.Inhalt:=Tiere[Wüste[i,j]];
Käfig.voll:=true;
Wüste[i,j]:=KEINER_INDEX;
exit; { Da der Käfig schon voll ist }
end; { Man könnte aber auch mit }
{ dieser Procedure alle Löwen einfangen. }
WriteLn('Achtung! Kein Löwe gefunden, wie wärs mit einem Kamel ?');
end;
begin;
Init; { Wüste, Tiere werden eingestellt. }
Löwen_Fang;
if (Käfig.voll) then WriteLn(' Ok,der Löwe ist im Käfig.')
else WriteLn('Achtung! Kein Löwe gefunden, durch "+
'Abänderung in KAMEL_INDEX wäre vielleicht"+
#10#13'ein Kamel möglich ?');
end.
Sogar als Shellscript geht es schon:
#!/bin/sh
for $tier in $Wüste
do
if [ $tier = $Löwe ]
then mv $tier $Käfig; exit 0
fi
done

|
 |
|

|